吐血整理！临床预测模型十大回归分析👍

回归分析在临床研究中的应用非常广泛，扮演着非常重要的角色。回归分析的目的和套路基本上差不多，通常用于：

（1）探索危险因素，比如疾病发生或临床结局的影响因素有哪些？

（2）定量分析影响因素对结局的影响，比如血糖和血脂有可能影响高血压病人的结局，哪个影响更大一些？

（3）校正混杂因素，比如饮食模式是结直肠癌的影响因素，但肥胖可能是影响两者关系的混杂因素，需要进行校正，观察饮食模式对结直肠癌的真实效应；

（4）预测风险概率，即根据已知的危险因素去预测临床结局的发生概率。

本期给大家整理了一些常见回归分析的定义以及使用场景，近期在学习或者想学习临床预测模型的同学一定要存好了！

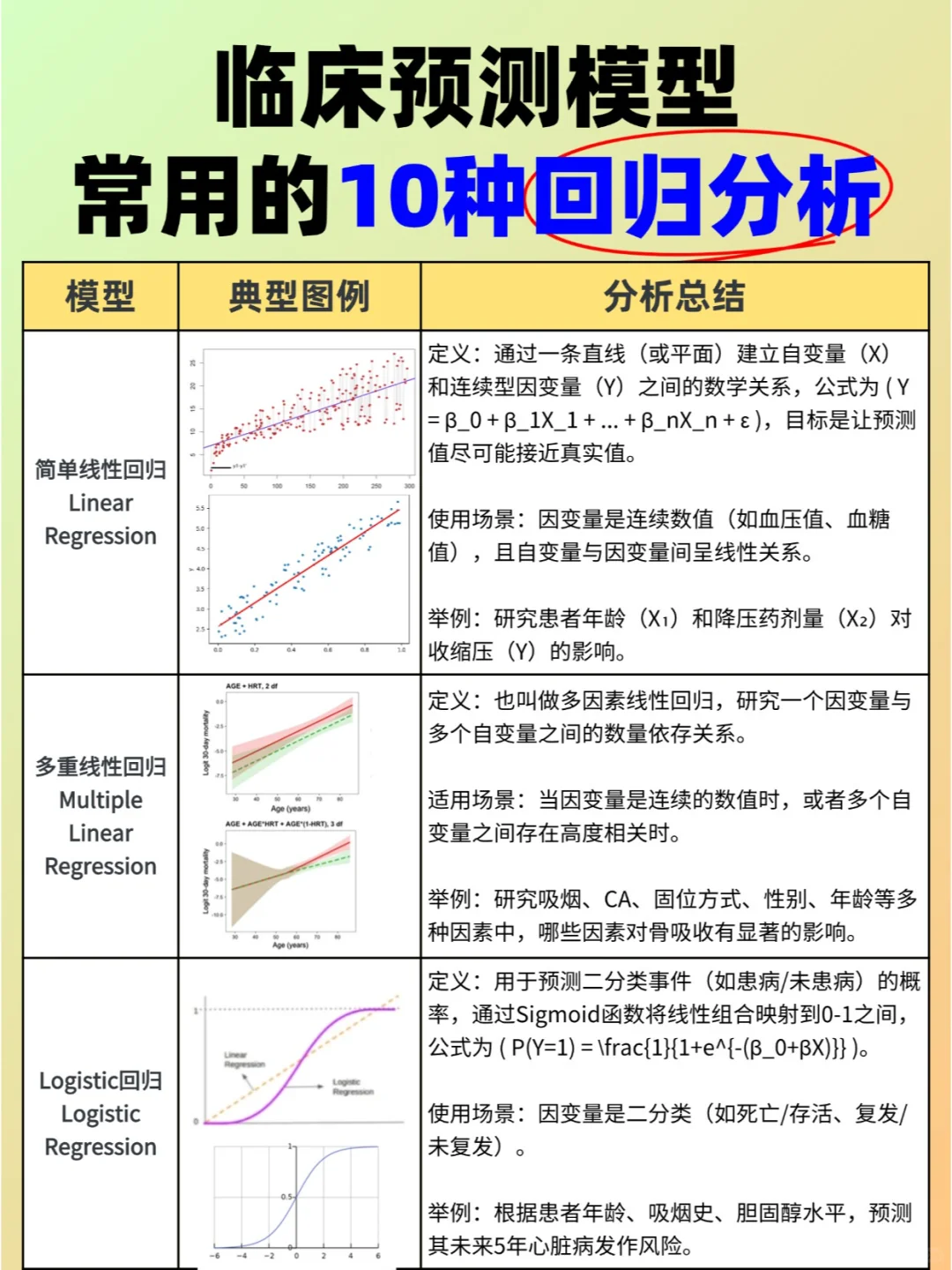
1. 线性回归（Linear Regression）

2. Logistic回归（Logistic Regression）

3. Cox比例风险回归（Cox Regression）

4. 泊松回归（Poisson Regression）

5. 负二项回归（Negative Binomial Regression）

6. 有序Logistic回归（Ordinal Logistic Regression）

7. 多项Logistic回归（Multinomial Logistic Regression）

8. 岭回归（Ridge Regression）

9. Lasso回归（Least Absolute Shrinkage and Selection Operator）

10. 分位数回归（Quantile Regression）

通过结合临床问题类型（连续/分类/生存/计数）和数据特征（共线性、维度、分布），选择合适回归方法可提升预测模型的准确性与解释性。

学临床预测模型，我们经常会听到各种回归分析，那么到底什么是回归？那么多回归又该如何进行区分呢？

🔹 什么是回归？

“回归”一词最早由英国生物统计学家 S.F.Galton（1885） 提出，他发现高个子父代的子代平均身高不是更高，而是稍矮；相反，矮个子父代的子代平均身高并不是更矮，而是稍高于其父代水平。他把这种 身高趋向种族稳定 的现象称为“回归”。

目前回归的含义已演变成 变量之间某种数量依存关系，简单来说：通过一堆已知的数据，找到“变量之间的套路”，然后用这个套路去预测未来。

🎯 举个例子：

假设你想知道 “一个人的年龄” 和 “他每天喝奶茶的量” 有什么关系。

你调查了 100 个人，记录他们的年龄和每天喝奶茶的杯数。回归分析可以帮你算出一个公式，比如：

📌 奶茶杯数 = 0.5 × 年龄 – 2

这个公式告诉你：年龄越大，奶茶喝得越少。（假设公式里年龄的系数是正数则是相反趋势）

于是你就能预测：一个 30 岁的人，大概每天喝 0.5 × 30 – 2 = 13 杯奶茶（当然，这只是举例，别当真😂）。

🔹 回归分析在临床中的应用

回归分析在 临床研究中的应用非常广泛，通常用于：

1️⃣ 探索危险因素，比如疾病发生或临床结局的影响因素。
2️⃣ 定量分析影响因素对结局的影响，如血糖和血脂对高血压患者结局的影响，哪个影响更大？
3️⃣ 校正混杂因素，比如 饮食模式是否影响结直肠癌，但肥胖可能是影响两者关系的混杂因素，因此需要校正。
4️⃣ 预测风险概率，即根据已知的危险因素，预测临床结局的发生概率。

🔹 常见的回归分析方法详解

📌 1. 线性回归（Linear Regression）

定义：线性回归的因变量（Y）是定量变量，自变量（X）可以是连续变量或分类变量。
使用场景：当因变量是 连续数值（如血压、血糖），且自变量和因变量之间呈线性关系时使用。
举例：研究 患者年龄（X₁）和降压药剂量（X₂）对血压（Y）的影响。

📌 2. Logistic 回归

定义：用于 预测二分类事件（如疾病/未患病），通过 Sigmoid 函数将数值结果映射到 0-1 之间。
使用场景：当因变量是 二分类变量（如死亡/存活、复发/未复发） 时使用。
举例：根据 患者年龄、吸烟史、胆固醇水平 预测 其未来 5 年心脏病发生风险。

📌 3. Cox 比例风险回归

定义：分析 事件发生时间（如死亡时间） 与多个预测因素的关系，核心是风险函数 h(t) = h₀(t)e^(βX)，假设风险比 随时间恒定。
使用场景：用于 处理生存数据（如 癌症患者生存期分析）。
举例：研究 肺癌患者的肿瘤大小（X₁）和化疗方案（X₂）对生存时间的影响。

📌 📢 注意： Cox 回归适用于 删失数据（即部分患者在研究结束时仍存活，无法确定其最终生存时间）。

📌 4. 泊松回归

定义：用于 计数型因变量（如住院次数），假设事件发生次数服从泊松分布（方差=均值）。
使用场景：当因变量是 低频、非负整数（如门诊次数、药物不良反应次数） 时使用。
举例：分析 哮喘患者过去 1 年内的急诊次数与空气污染程度、用药依从性的关系。

📌 5. 负二项回归

定义：泊松回归的扩展，允许因变量方差 > 均值（即过度离散），适用于波动较大的计数数据。
使用场景：当因变量是 高频或波动性强的计数数据（如感染发作次数、门诊复诊次数） 时使用。
举例：研究 糖尿病患者每年因高血糖住院次数与血糖控制水平的关系。

📌 6. 有序 Logistic 回归

定义：处理 因变量为有序多分类（如 疾病分期 I/II/III），假设 不同类别之间“阈值”效应相同。
使用场景：预测 分级分类的结局变量（如患者疾病严重程度 I/II/III）。
举例：研究 糖尿病患者的 BMI、血糖水平与糖尿病分期的关系。

🔹 总结：如何选择合适的回归模型？

回归方法	因变量类型	适用情况
线性回归	连续变量（如血压、血糖）	变量间存在线性关系
Logistic 回归	二分类变量（如生病/未生病）	预测事件的概率
Cox 回归	存活时间（如生存期）	处理删失数据
泊松回归	计数型变量（如住院次数）	低频事件
负二项回归	计数型变量（如复诊次数）	过度离散数据
有序 Logistic 回归	有序分类变量（如疾病分期）	预测多级分类结局

💡 结论

回归分析在医学研究中至关重要，不仅可以用于探索影响疾病的风险因素，还可以预测患者的结局或事件发生概率。
选择合适的回归方法，是确保研究结果科学合理的关键！ 🎯

🔹 6. 有序 Logistic 回归

定义：处理因变量是 有序多分类（如 疾病分期 I/II/III），假设不同类别之间的“阈值”效应相同。
使用场景：当因变量是 有序等级（如疼痛程度：轻度/中度/重度）时使用。
举例：预测 慢性肾病患者的疾病分期（1-5 期） 与 血肌酐、尿蛋白水平的关系。

🔹 7. 多项 Logistic 回归

定义：处理因变量是 无序多分类（如 肿瘤亚型 A/B/C），为每个类别建立 独立的 Logit 方程。
使用场景：当因变量是 无序多类别（如 病理分型、治疗方案选择）时使用。
举例：根据 基因表达数据，预测 乳腺癌的分子亚型（Luminal A/B、HER2+、三阴性）。

🔹 8. 岭回归（Ridge Regression）

定义：通过引入 L2 正则化（系数平方惩罚项），解决 多重共线性 问题（自变量高度相关）。
使用场景：当 自变量数量多且高度相关（如基因表达数据、影像组学特征）时使用。
举例：从 100 个基因表达变量 中筛选 与肺癌转移相关的关键基因。

🔹 9. Lasso 回归

定义：通过 L1 正则化（系数绝对值惩罚项）自动进行变量选择，可将部分系数压缩为 0。
使用场景：当数据是 高维数据，需要 简化模型（如影像组学、基因组学）时使用。
举例：从 500 个候选影像特征 中筛选 10 个关键特征构建脑肿瘤预后模型。

🔹 10. 分位数回归（Quantile Regression）

定义：分析因变量在 不同分位数（如中位数、90%分位数） 下与自变量的关系，关注极端值而非均值。
使用场景：当因变量 分布不对称或有异质性（如 收入、医疗费用）时使用。
举例：研究 极端高血糖（90%分位数）患者与普通患者的危险因素差异。

🔹 回归方法选择对照表

回归方法	核心目的	典型数据特征
线性回归	预测连续值	因变量连续，线性关系
Logistic 回归	预测二分类概率	因变量二分类
Cox 回归	分析生存时间	含删失的生存数据
泊松回归	预测低频计数	计数数据，方差≈均值
负二项回归	预测高频波动计数	计数数据，方差>均值
有序 Logistic	预测有序多分类	因变量等级（如 I/II/III 期）
多项 Logistic	预测无序多分类	因变量为互斥类别（如 A/B/C 型）
岭回归/Lasso	处理共线性或高维数据	自变量多且相关性高
分位数回归	分析极端值或异质性效应	因变量分布偏态或长尾

📢 结论

📌 学临床预测模型，一定要自己亲自操作，光看是学不会的！
📌 最有效的方法就是 参加项目，在项目中锻炼学习。
📌 如果你想今年入门临床预测模型，但 缺乏合适的题目或资源，建议寻找 靠谱的项目组，在 临床大佬 的带领下 从 0 到 1 选题落地！ 🚀 🚀 🚀